KELOMPOK 9
Kelompok 9 :
- Salsabilla Khaeranie (33)
- Sheysa Radisty Helindra (34)
- Zahra Lisea Jupika (35)
kelas X.B
Mata Pelajaran : Matematika
1) Materi : 13. Peserta didik mampu Menyelesaikan masalah kontekstual yang terkait dengan barisan geometri
Oleh : Sheysa Radisty Helindra (34)
> pengertian :
Barisan geometri adalah pola bilangan atau urutan bilangan yang memiliki perbandingan atau rasio tetap antarsukunya.
> rumus :
Secara matematis, rumus suku ke-n barisan geometri adalah sebagai berikut.
Dengan ketentuan:
Un = suku ke-n;
a = suku ke-1 atau U1;
n = letak suku yang dicari; dan
r = rasio atau perbandingan antara Un+1 dan Un.
> contoh soal :
Setelah kamu tahu rumus untuk mencari suku-n, cobalah hitung berapa jumlah amoeba yang dihasilkan pada pembelahan ke-10? Jumlah awal amoebanya adalah satu, ya.
Mula-mula, kamu harus membuat barisan geometri dari pembelahan amoeba seperti berikut.
1, 2, 4, 8, 16, 31, …, …
Dari barisan di atas, diketahui:
a = U1 = 1
r = 2 : 1 = 2 atau 4 : 2 = 2
n = 10
dengan demikian:
Jadi, banyaknya amoeba di pembelahan ke-10 adalah 512.
> latihan dan pembahasan :
Soal 1
Diberikan suatu barisan 3, 9, 27, 81... Diketahui barisan tersebut merupakan barisan geometri. Tentukan suku ke-5 dari barisan tersebut.
Pembahasan 1
Seperti yang kita ketahui, barisan geometri memiliki rasio konstan antara dua suku berurutan. Oleh karena itu, kita cari rasio dari barisan tersebut lebih dulu.
r = u2/ u1 = 9/3
= 3
Setelah mengetahui bahwa rasio tersebut adalah 3 maka kita masukkan dalam rumus suku ke-n
U5 = 3 x 3 (5-1)
= 3 x 3(4)
= 3 x 81
= 243
Jadi, suku ke-5 dari barisan geometri tersebut adalah 243
Soal 2
Diberikan barisan geometri pecahan sebagai berikut : 1/2, 1/4, 1/8, 1/16,..... Tentukan suku ke-6 dalam barisan tersebut.
Pembahasan 2
Dalam barisan geometri dengan angka pecahan, kita juga dapat menggunakan rumus umum barisan geometri untuk mencari suku ke-n. Rumus tersebut tetap berlaku, hanya saja kita harus memahami bagaimana mengaplikasikannya pada angka pecahan.
Diketahui:
a1 = ½ dan a2 = 1/4
Maka rasio barisan tersebut adalah 1/4 : 1/2 = ½
Sekarang kita bisa menggunakan rumus ini untuk mencari suku ke-6 setelah mengetahui bahwa rasio barisan tersebut adalah 1/2.
U6 = 1/2 x (½ (6-1))
U6 = 1/2 x (½ (5))
U6 = 1/2 x 1/32
U6 = 1/64
Jadi, suku ke-6 dalam barisan geometri tersebut adalah 1/64
soal 3
Jika diketahui barisan geometri dengan suku ke-2 = 80 dan suku ke-6 = 5. Tentukan tiga suku pertama dari barisan geometri tersebut.
pembahasan 3
Suku ke-2 = U2 = ar = 80 ... persamaan 1.
Suku ke-6 = = 5 ... persamaan 2.
Untuk mencari rasio barisan geometrinya, kita dapat mensubstitusikan persamaan 1 ke persamaan 2.
Sehingga, didapatkan rasio barisan geometri tersebut adalah ½. Setelah mendapatkan rasionya, kita harus menghitung suku pertamanya (a).
Maka, didapatkan bahwa suku pertama barisan geometri tersebut adalah 160. Setelah diketahui rasio dan suku pertamanya, kita dapat menghitung tiga suku pertama.
Sehingga, tiga suku pertama dari barisan geometri tersebut adalah 160, 80, dan 40.
soal 4
Tuliskan dua suku berikutnya dari barisan bilangan di bawah ini.
1/8, ¼, ½, … , …
25, 5, 1, … , …
pembahasan 4
1/8, ¼, ½, … , …
Rasio barisan geometri di atas = .
½ x 2 = 1
1 x 2 = 2
Sehingga, dua suku selanjutnya adalah 1 dan 2.
25, 5, 1, … , …
Rasio barisan geometri di atas = 25/5 = 5
1 : 5 = 1/5
1/5 : 5 = 1/25
Sehingga, dua suku selanjutnya adalah 1/5 dan 1/25.
2) Materi : 34. Peserta didik mampu Menentukan panjang sisi-sisi pada suatu segitiga siku-siku dengan menggunakan teorema pythagoras
Oleh : Sheysa Radisty Helindra (34)
> pengertian :
Rumus Pythagoras adalah salah satu rumus matematika yang paling penting dan sering digunakan. Teorema pythagoras adalah salah satu pembahasan yang pasti akan muncul dalam pelajaran matematika. Rumus ini digunakan untuk mencari panjang sisi miring (hipotenusa) pada segitiga siku-siku. Materi ini menjelaskan tentang hubungan antara tiga sisi segitiga siku-siku.
> rumus :
Dalam bentuk matematis, rumus pythagoras dapat ditulis sebagai:
c² = a² + b², di mana c adalah panjang hipotenusa, dan a dan b adalah panjang kedua sisi yang pendek.
Rumus diatas digunakan untuk mencari sisi miring atau sisi terpanjang pada segitiga siku-siku. Lalu, bagaimana cara mencari panjang sisi yang lainnya?
Untuk mencari sisi depan dan sisi sampingnya, kamu dapat menggunakan rumus berikut:
a² = c² - b² (untuk mencari sisi depan)
b² = c² - a² (untuk mencari sisi samping)
> contoh soal :
Sebuah segitiga siku-siku memiliki sisi alas (a) sepanjang 9 cm dan tinggi (b) 12 cm. Berapa panjang sisi miring segitiga siku-siku ini jika dihitung dengan rumus Pythagoras?
Jawab:
a = 9cm
b = 12 cm
c = ?
Cara mencari sisi miring (c) segitiga siku-siku dengan menggunakan rumus Pythagoras:
c² = a² + b²
c² =12 ² + 9²
c² = 144 + 81
c² = 225
c = √225
c = 15 cm
> latihan dan pembahasan :
Soal 1
Tentukan jenis segitiga yang memiliki panjang sisi 5 cm, 7 cm dan 8 cm?
Jawab:
Sisi terpanjang adalah 8 cm, maka:
a = 8 cm, b = 7 cm, c = 5 cm
a² = 82 = 64
b²+ c² = 72 + 52
b²+ c² = 49 + 25
b²+ c² = 74
Dikarenakan a² < b²+ c² , maka dapat disimpulkan bahwa segitiga tersebut adalah segitiga lancip.
soal 2
Sebuah segitiga siku-siku memiliki sisi alas (a) sepanjang 5 cm dan tinggi (b) 12 cm. Berapa panjang sisi miring atau hipotenusa segitiga siku-siku ini jika dihitung dengan rumus Pythagoras.
Jawab:
a = 5 cm
b = 12 cm
c = ?
Berikut cara mencari sisi miring (c) segitiga siku-siku dengan menggunakan rumus Pythagoras:
c2 = a2 + b2
c2 = 5 kuadrat + 12 kuadrat
c2 = 25 + 144
c2 = 169
c = √169
c = 13 cm
Soal 3
Sebuah segitiga siku-siku diketahui memiliki sisi alas (a) 6 cm dan sisi miring (c) 10 cm. Hitung dengan rumus Pythagoras tinggi (b) dari segitiga siku-siku ini.
Jawab:
a = 6 cm
c = 10 cm
b = ?
Berikut cara mencari tinggi (b) segitiga siku-siku dengan menggunakan rumus Pythagoras.
c2 = a2 + b2
b2 = c2 - a2
b2 = 10 kuadrat - 6 kuadrat
b2 = 100 - 36
b2 = 64
b = √64
b = 8 cm
Soal 4
Segitiga ABC memiliki luas 30 sentimeter persegi dengan siku-siku di A. Panjang sisi miringnya (a) adalah 13 dan sisi tegaknya (b) adalah 12.
Carilah panjang sisi mendatar/alas (c) dengan menggunakan teorema pythagoras?
Carilah panjang sisi mendatar/alas (c) dengan menggunakan rumus luas.
Jawaban:
a kuadrat = b kuadrat + c kuadrat
13 kuadrat = 12 kuadrat + c kuadrat
169 = 144 + c kuadrat
c = akar 25
c = 5 cm
Soal 5
Sisi miring segitiga siku-siku adalah 16 cm dan salah satu sisi segitiga tersebut adalah 8 cm. Temukan ukuran sisi ketiga menggunakan rumus pythagoras.
Diketahui:
Sisi miring= 16 cm
Mari kita anggap sisi segitiga sebagai tinggi tegak lurus= 8 cm
Ditanyakan: Sisi ketiga ?
Jawab:
Sisi miring2= Alas2 + Tinggi2
162= B2+82
B2= 256-64
B2= √192= 13.856 cm
Soal 6
Sebuah segitiga siku-siku ABC dengan B sebagai sudut siku-siku. Apabila panjang AB = 16 cm serta sisi BC = 12 cm. Maka hitunglah panjang sisi AC pada segitiga tersebut.
Diketahui:
AB= 16 cm
BC= 12 cm
Ditanya: Sisi AC ?
Jawab:
c&³2;= a&³2;+b&³2;
c&³2;= 12&³2;+16&³2;
c&³2;= 144+256
c&³2;= 400
c= √400
c= 20 cm
3) Materi : 33.Peserta didik mampu Menggunakan sifat-sifat persamaan eksponensial (berbasis sama) dalam menyelesaikan masalah
Oleh : Salsabilla Khaeranie (33)
> pengertian :
Eksponen merupakan bentuk perkalian suatu bilangan dengan dirinya sendiri sebanyak pangkatnya. Persamaan eksponen adalah persamaan bilangan berpangkat yang memuat variabel di bagian pangkatnya. Oleh karena memuat suatu variabel, maka pangkatnya bisa dinyatakan sebagai suatu fungsi, misal f(x) atau g(x) untuk pangkat bervariabel x. Contoh persamaan eksponen adalah 32x – 4 = 32.
> rumus :
> contoh soal :
Tentukan penyelesaian dari persamaan ekponensial berikut ini 22x-7 = 81-x jawab : Pertama-tama yang perlu kamu lakukan yaitu menyamakan basis pada kedua ruas [ruas kanan dan ruas kiri] seperti berikut: 22x-7 = 81-x 22x-7 = (23)1-x 22x-7 = 23-3x Nahhhh karena basismya telah sama, maka dengan mudah kita dapat menentukan nilai x-nya seperti
2x – 7 = 3 – 3x 5x = 10 x = 2 Sehingga kita peroleh x = 2
2. Jika a dan b bilangan bulat positif yang memenuhi ab = 220 – 219 , maka nilai a + b = …
jawab:
Dengan menggunakan sifat pangkat dan sifat distributif, diperoleh
ab = 220 – 219 ab = 219 . 2 – 219 ab = 219 . (2-1) Dari sini, kita peroleh a = 2 dan b = 9 sehingga a + b = 2 + 19 = 21
> latihan dan pembahasan :
1. Tentukan penyelesaian dari persamaan eksponensial berikut ini 22x-7 = 81-x
Jawaban:
22x-7 = 81-x
22x-7 = (23)1-x
22x-7 = 23-3x
Jadi, cara menentukan nilai x-nya seperti berikut ini.
2x – 7 = 3 – 3x
5x = 10
x = 2
Sehingga kita peroleh x = 2
2. Jika a dan b bilangan bulat positif yang memenuhi ab = 220 – 219 , maka nilai a + b = …
Jawaban:
Dengan menggunakan sifat pangkat dan sifat distributif, diperoleh:
ab = 220 – 219
ab = 219 . 2 – 219
ab = 219 . (2-1)
Dari sini, diperoleh a = 2 dan b = 9 sehingga a + b = 2 + 19 = 21
3. Tentukan nilai x yang memenuhi persamaan eksponensial 3ˣ⁺²+3ˣ=10
Jawaban:
3ˣ⁺²+3ˣ=10
3ˣ(3²+1)=10
3ˣ(10)=10
3ˣ = 1
3ˣ=3⁰
x=0
4. Tentukan himpunan penyelesaian dari 9 x²+x = 27 x²-1
Jawaban:
9 x²+x = 27 x²-1
3 2(x²+x) = 3 3(x²-1)
2 (x2+x) = 3 (x2-1)
2x2 + 2x = 3x2 – 3
x2 – 2x – 3 = 0
(x – 3) (x + 1) = 0
x = 3 atau x = -1
Jadi, himpunan penyelesaiannya adalah { -1,3 }
5.Tentukan nilai x dari persamaan 3^5-1 – 27^x+3 = 0
Jawab:
3^5-1 – 27^x+3 = 0
3^5-1 = (3^3)^x+3
3^5-1 = 3^3x+9
5x-1 = 3x + 9
2x = 10
X = 5
pembahasan
Bentuk Umum Persamaan Eksponen
Adapun bentuk umum persamaan eksponen adalah sebagai berikut.
af(x) = ag(x)
Dengan:
a = basis (bilangan pokok); dan
f(x) dan g(x) = pangkat atau eksponen.
Quipperian harus ingat ya, jika bentuk umum persamaan eksponen pasti memuat variabel di bagian pangkatnya. Jika variabel bukan di bagian pangkat, maka persamaannya bukan termasuk persamaan eksponen, contoh:
2x + 1 = 25 → persamaan eksponen
(2x + 1)2x = xx – 1 → persamaan eksponen
x2 + 2 = 0 → bukan persamaan eksponen karena variabelnya terletak di bagian basis.
Meskipun memiliki bentuk umum tertentu, namun persamaan eksponen itu beragam seperti persamaan eksponen bentuk akar, persamaan eksponen sederhana, persamaan eksponen tak sederhana, dan lainnya.
4) Materi : 12.Peserta didik mampu Menentukan rumus suku ke-n suatu barisan geometri
Oleh : Salsabila Khaeranie (33)
> pengertian :
Barisan geometri terbentuk dari bilangan yang memiliki pola tertentu. Pola tersebut membuat kita dapat menentukan suku bilangan tertentu (suku ke-n). Bagaimana cara menentukan rumus suku ke-n barisan geometri.
Untuk dapat menentukan rumus suku ke-n, kita harus memahami pola apa yang membentuk barisan geometri. Dilansir dari Cuemath, barisan geometri terbentuk dari suatu suku (kecuali suku pertama) dikalikan dengan bilangan konstan untuk mendapatkan suku berikutnya.
> rumus :
> contoh soal :
Tentukan suku ke-10 dari barisan geometri 3,6,12!
Jawab:
a = 3
r = 6/3 = 2
n = 10
Un = arn-1
maka:
U10 = 3(2)10-1
U10 = 3(2)9
U10 = 3 x 512
U10 = 1.536
Jadi, nilai U10 adalah 1.536
2. Tentukan rumus suku ke-n dari barisan geometri 3,6,12,24,...
Jawab:
Un = a.rn-1
Un = 3 x 2n-1
> latihan dan pembahasan :
1.Tentukan suku ke-10 dari barisan geometri 3, 6, 12!
Diketahui:
a = 3
r = 6:3 = 2
n = 10
Jawab:
Un= a x r^(n-1)
U10 = 3 x 2^(10-1)
U10 = 3 x 2^(9)
U10 = 3 x 512
U10 = 1.536
Jadi, nilai U10 dari barisan geometri adalah 1.536.
2.Tentukan rumus suku ke-n dari barisan geometri 6, 12, 24,...
Jawab:
Un= a x r^(n-1)
Un = 6 x 2^(n-1)
Jadi, rumus barisan geometri adalah Un = 6 x 2^(n-1).
3.Tentukanlah rasio (r), jika diketahui suku pertama dari barisan geometri adalah 3 dan suku ke-4 dari barisan tersebut adalah 24!
Diketahui:
U1 = a =
3U4 = 24
Jawab:
Un= a x r^(n-1)
U4 = a x r^(4-1)
24 = 3 x r^3
r^3 = 24:3
r^3 = 8
r= ∛8
r = 2
Jadi, rasio dari barisan geometri tersebut adalah 2.
4.Tentukanlah rasio (r), jika diketahui suku pertama dari barisan geometri adalah 3 dan suku ke-4 dari barisan tersebut adalah 24!
Jawab:
Diketahui bahwa, U1 = a = 3 dan U4 = 24. Maka rasionya dapat diperoleh dari penurunan suku ke-4, yakni sebagai berikut:
Un = a.rn-1
U4 = a.r4-1
24 = 3r3
r3 = 24/3
r3 = 8
r3 = 23
r = 2
Jadi, rasio dari barisan geometri tersebut adalah 2.
5.Diketahui barisan geometri dengan suku-5 yaitu 162 dan suku ke-2 = -6. Maka rasio barisan tersebut adalah ....
Jawab:
Diketahui: U5 = 162, U2 = -6.
Tentukanlah rasio dengan menggunakan suku-suku yang telah diketahui:
U5 = a x r4 = 162 ...... (1)
U2 = a x r = -6 ...... (2)
Dari persamaan (1) dan (2) akan diperoleh:
a x r4 = 162
a x r = -6 :
-----------------
r3 = -27
r3 = -(3)3
r = -3
Jadi, rasio dari barisan geometri tersebut adalah -3
5) Materi : 14. Deret Geometri
Oleh: Zahra Lisea Jupika X-B (35)
> pengertian :
Geometri adalah ilmu yang mempelajari hubungan antara objek-objek geometri, seperti titik, garis, bangun, dan sudut. Geometri merupakan cabang ilmu tertua dalam Matematika.
> rumus :
Keterangan:
Sn = Jumlah suku ke – n dari deretan geometri
a = Suku pertama
r = Rasio
•Pembuktian Rumus Deret Geometri.
Berikut ini adalah pembuktian rumus deret geometri, khususnya pada deret turun untuk r < 1.
⇔ Sn = U1 + U2 + U3 + U4 + … + Un
⇔ = a + ar + ar2 + ar3 + …+ arn-1 ……………………… (1)
Nah, dari persamaan (1) tersebut, semua suku akan dikalikan dengan r, maka menjadi:
⇔ r.Sn = r (U1 + U2 + U3 + U4 + … + Un )
⇔ = r ( a + ar + ar2 + ar3 + …+ arn-1)
⇔ = a + ar + ar2 + ar3 + …+ arn ………………… (2)
Lalu, dari persamaan (1) dan (2) tersebut, akan diperoleh penghitungan berikut ini:
Sn = a + ar + ar2 + ar3 + …+ arn-1
r.Sn = ar + ar2 + ar3 + ar4+….. + arn
————————————————————— –
Sn – r.Sn = a + (-arn )
(1-r) Sn = a – arn
Sehingga akan diperoleh rumus:
> contoh soal :
1.Tentukan jumlah 9 suku pertama dari deret geometri 3 + 6 + 12 + 24 + 48 + …
Penyelesaian:
Diketahui: a = 3
Ditanya: S9
Jawab:
2. Seutas tali dibagi menjadi 6 bagian dengan ukuran panjang membentuk deret geometri; jika bagian yang paling pendek 3 cm dan yang terpanjang 96 cm, tentukanlah ukuran panjang tali tersebut.
Penyelesaian:
Diketahui: Un = 96; a = 3; n = 6
Ditanya: S7
Jawab:
Un = arn-1
⇔ 96 = 3 . r5
⇔ r5 = 32
⇔ r = 2
Karena r > 1, maka rumus penghitungan yang berlaku adalah
Jadi, ukuran panjang tali tersebut adalah 189 cm.
> latihan dan pembahasan :
1. Dalam suatu deret membentuk 4 + 2 + 1 + 1/2 + ¼ ….. Hitunglah berapa jumlah barisan geometri dari susunan suku tersebut!
Pembahasan:
Diketahui a = 4 dan r = ½
Ditanyakan: Sn = ?
Jawab:
Sn = a / (1 – r) = 4 / (1 – ½) = 4 / (½) = 4 x 2 = 8
Jadi, jumlah barisan geometri dari susunan bilangan tersebut adalah 8.
2. Apabila diketahui suatu deret angka 5 + 15 + 45 + … Maka, berapakah jumlah enam suku pertama dari deret tersebut?
Pembahasan:
Diketahui: a = 5, r = 3
Sehingga jumlah enam suku pertama yakni...
Jawab:
Sn = a (rn – 1) / r – 1
S6 = 5 (36 – 1) / 3 – 1 = 3.640 / 2 = 1.820
Jadi, jumlah dari 6 suku pertama barisan geometri tersebut adalah 1.820.
3. Dalam suatu susunan bilangan yang membentuk deret geometri, diketahui bahwa suku pertamanya 3 serta suku ke sembilan adalah 768. Jadi, berapa suku ke-7 dari deret bilangan tersebut?
Pembahasan:
Diketahui a = 3, U9 = 768
Jawab:
Un = a(rn-1)
768 = 3 (r9-1)
768 = 3 x r8
r8 =768/3
r8 = 256
r8 = 28
r = 2
Maka suku ketujuh adalah U7 = 3 x 26 = 194.
4. Jumlah dari 400 + 200 + 100 + 50 + 25 + 12,5 = ...J
Jawab:
a = 400
r = 200 : 400
= 100 : 200= ½
n = 6
Jadi jumlah dari 500 + 200 + 100 + 50 + 25 + 12,5 = 787,5
5. Rani memiliki seutas tali. Lalu, tali tersebut dipotong menjadi 5 bagian dengan ketentuan, setiap potongan merupakan kelipatan potongan sebelumnya dan nilai kelipatan itu selalu tetap. Potongan tali yang paling pendeknya adalah 3 cm dan potongan tali terpanjangnya 243 cm. Berapakah panjang tali mula-mula?
Pembahasan:
Diketahui:
U1 = a = 3 cm
U5 = 243
Ditanya: Sn =...?
Jawab:
Mula-mula, kamu harus mencari rasio setiap potongan tali tersebut. Maksud tanda (/) adalah per (-)
U5/U1 = 243/3
U5/U1 = 81
r4 = 81
r = 3
Kemudian, tentukan panjang tali menggunakan rumus deret geometri untuk r>1
Sn= a (rn-1)/ r-1
= 3 (35-1)/ 3-1
= 3 (242)/2
= 363 cm
Jadi, panjang tali Rani mula-mula adalah 363 cm atau 3,63 m.
6) Materi: 35. Segitiga Siku Siku
Oleh: Zahra Lisea Jupika X-B (35)
> pengertian :
• Segitiga siku-siku adalah sebuah segitiga di mana salah satu sudutnya membentuk sudut siku-siku atau 90 derajat.
• Segitiga siku siku memiliki dua sisi yang saling tegak lurus. Segitiga siku siku tidak memiliki simetri putar dan simetri lipat.
• Hubungan antara sisi dan sudut segitiga siku-siku adalah dasar untuk trigonometri.
• Sisi yang berseberangan dengan sudut siku-siku disebut sisi miring atau hipotenusa. Sisi lainnya adalah alas dan tinggi.
Ada enam buah perbandingan trigonometri yaitu sinus, cosinus, tangen, cotangen, cosecan, dan juga secan.
Untuk mengukur salah satu sisi tersebut maka diperlukan Teorema Phytagoras:
"Sisi miring atau sisi terpanjang dalam segitiga siku–siku sama dengan kuadrat sisi-sisi lainnya."
-MENENTUKAN SISI DEPAN, SISI MIRING UNTUK SUATU SUDUT LANCIP (α) PADA SUATU SEGITIGA SIKU SIKU-
Untuk memahami bagaimana menentukan sisi depan, sisi samping, dan sisi miring dalam sebuah segitiga siku-siku, kita perlu memahami dasar-dasar geometri dan trigonometri.
Sisi Miring (Hipotenusa)
- Sisi miring adalah sisi terpanjang dalam segitiga siku-siku dan selalu berhadapan dengan sudut siku-siku.
Sisi Depan
- Sisi depan adalah sisi yang berhadapan langsung dengan sudut lancip yang sedang dibahas.
Sisi Samping
- Sisi samping adalah sisi yang membentuk sudut lancip dengan sisi miring
> rumus :
Berdasarkan teorema phytagoras diperoleh rumus sebagai berikut untuk mencari sisi miring atau terpanjang pada segitiga siku-siku:
c² = a² + b²
Lalu, bagaimana cara untuk mencari sisi lainnya yaitu sisi depan dan sisi samping? Maka dengan demikian, rumusnya menjadi seperti berikut ini:
a² = c² – b² (mencari sisi depan)
b² = c² – a² (mencari sisi samping)
Perlu juga diketahui tentang pola triple phytagoras, dengan menghafalkan tripel pythagoras bisa lebih cepat menyelesaikan soal tanpa perlu menghitung. Di awal sudah dijelaskan bahwa ditemukan sebuah fakta pola segitiga dengan panjang sisi 3, 4, dan 5 satuan panjang akan membentuk segitiga siku siku.
> contoh soal :
1. YouTuber Jerome Pollin beberapa waktu lalu membuat sebuah tantangan kepada para influencer dan konten kreator untuk menyelesaikan soal matematika. Salah satunya, menghitung sisi segitiga siku-siku. Berikut ini soalnya:
Ada segitiga siku siku siku, panjang sisi miringnya adalah 15 cm, panjang salah satu sisi lainnya adalah 9 cm (mendatar), maka panjang sisi satunya lagi adalah?
Diketahui:
c: 15 cm (sisi miring)
b: 9 cm (sisi mendatar)
Ditanya: Sisi tegak a?
Jawaban:
Karena yang dicari adalah sisi tegak maka rumus yang digunakan a² = c² – b².
a² = c² – b²
a² = 15² – 9²
a² = 225-81
a² = 144
a= √144
a= 12 cm
Jadi, sisi tegak (a) adalah 12 cm
2. Sebuah segitiga siku-siku memiliki sisi tegak 9 cm dan sisi depan 12 cm. Berapakah sisi miring dari segitiga siku-siku tersebut?
Diketahui:
Sisi tegak (b) = 9 cm
Sisi depan (a) = 12 cm
Ditanya: Sisi miring (c) = ?
Jawab:
c² = a² + b²
c² =12 ² + 9²
c² = 144 + 81
c² = 225
c = √225
c = 15 cm
Jadi, panjang sisi miring (c) adalah 15cm
> latihan dan pembahasan
1. Tentukan nilai a!
Pembahasan:
a² = c² – b² = 502 – 142 = 2.500 – 196 = 2.304
a = √2.304 = 48
Jadi, nilai a adalah 48 cm.
2. Sebuah segitiga siku-siku, hipotenusanya 4 √3 cm dan salah satu sisi siku-sikunya 2 √2 cm. Panjang sisi siku-siku yang lain adalah .... cm
Pembahasan:
Diketahui:
- Panjang hipotenusa/sisi miring = 4√3 cm (misal panjang AC)
- Panjang sisi yang lain = 2√2 cm (misal panjang BC)
Ditanya: sisi yang lain (misal panjang AB)
Jawab:
AB² = AC² - BC²
AB² = (4√3)² - (2√2)²
AB² = 48 - 8
AB² = 40
AB = √40
AB = √4.10
AB = 2√10
3. Panjang hepotenusa sebuah segitiga siku-siku sama kaki 16 cm dan panjang kaki-kakinya x cm. Nilai x adalah .... cm
Pembahasan:
Diketahui:
- Panjang hipotenusa/sisi miring = 16 cm
- Panjang sisi x = x (panjang kaki-kakinya)
Ditanya: panjang x...?
Jawab:
16² = x² + x²
16² = 2x²
256 = 2x²
128 = x²
√128 = x
√64.2 = x
8√2 = x
4. Segitiga PQR siku-siku di P. Jika panjang QR = 29 cm dan PQ = 20 cm, maka panjang PR adalah .... cm.
5. Panjang sebuah tangga 10 m disandarkan pada tembok sehingga ujung bawah tangga dari tembok 6 m. Jarak ujung atas tangga dari tanah adalah...





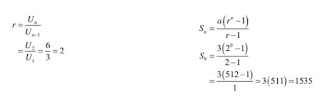
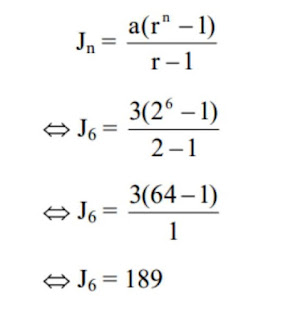





Komentar
Posting Komentar